La vida y la muerte de las estrellas
Original web-page: https://faculty.wcas.northwestern.edu/~infocom/The%20Website/pressure.html
David Taylor
Materia bajo presión
Para comprender las estrellas, debes comprender la presión. Desde el nacimiento hasta la muerte, la presión interna de una estrella creada por su propio peso es el factor más dominante en la vida de la estrella.
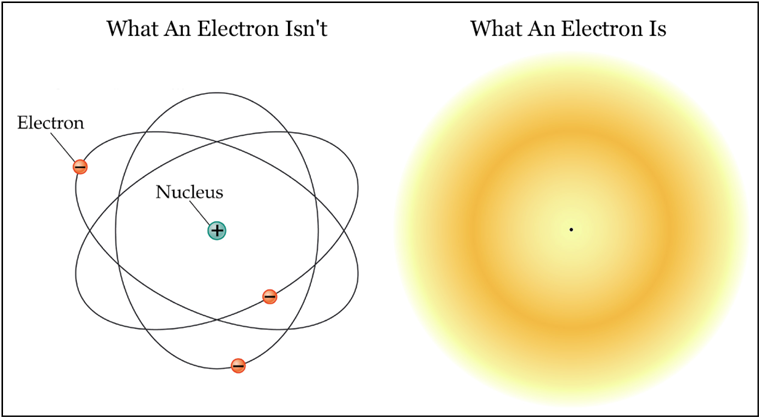
Suponga que toma un montón de arena y le agrega más arena. La pila se hará más grande. Uno podría imaginar que esto también es cierto para los planetas o las estrellas, y lo es, pero solo hasta cierto punto. La cuestión es que lo que llamamos “materia sólida” no es nada por el estilo a escalas microscópicas. La materia consta de átomos diminutos. Si pudieras expandir el núcleo de un átomo al tamaño de una canica, entonces pesaría tres mil millones de toneladas y el núcleo más cercano estaría a dos millas de distancia. Entre los núcleos sólo hay “nubes” de electrones ligeros. (Consulte la Imagen 1 para obtener más información sobre las nubes de probabilidad de electrones).
Mil millones de toneladas de canicas de media pulgada esparcidas a millas de distancia equivalen a una gran cantidad de espacio vacío, no a materia sólida. El factor que hace que la materia sea “sólida” es la fuerza electromagnética que opera entre los átomos. Esta fuerza, más las reglas de la mecánica cuántica, encierran a los átomos en los arreglos que a los humanos nos complace llamar “sólidos”, principalmente porque pueden resistir cualquier fuerza compresiva que nuestra tecnología pueda aplicar. Pero no lo son. Nada es sólido si le aplica suficiente presión. La idea de que más masa debe ser igual a un volumen mayor es cierta solo para objetos “pequeños” como el planeta Tierra, cuyo peso no es suficiente para comprimir demasiado sus núcleos. (Sin embargo, incluso para planetas más pequeños como Marte o la Tierra, las presiones centrales siguen siendo inmensas. La Tierra tiene un volumen aproximadamente un 20% menor de lo que cabría esperar, según su química, porque su peso ha comprimido su hierro central núcleo a aproximadamente el doble de la densidad del hierro que se encuentra en la superficie).
A medida que los planetas se vuelven más masivos, la tendencia a la compresión gravitacional aumenta hasta que finalmente, con una masa aproximadamente 1,7 veces mayor que la de Júpiter1 (540 masas terrestres), se llega a un punto crítico en el que el planeta deja de agrandarse. Más allá de este punto crítico2, agregar más masa a un planeta en realidad lo hace más pequeño porque la compresión creada por la masa adicional es mayor que el volumen de la masa adicional. (La Imagen 2 tiene más detalles).
Debido a que los planetas supermasivos combinan un radio decreciente con una masa creciente, sus densidades (masa dividida por volumen) son estratosféricas, muchas veces superiores a las del plomo. Las temperaturas y presiones centrales de los planetas supermasivos son tan inmensas que los átomos no pueden unirse entre sí, es decir, las rocas, el hielo y otros compuestos no pueden existir. Todo lo que puede tener son átomos individuales flotando. Por lo tanto, es más exacto pensar en los superplanetas como bolas de gas extremadamente comprimidas, en lugar de como un núcleo líquido o sólido con una atmósfera envuelta a su alrededor. La presión del núcleo también limita la masa de un planeta: el planeta muy denso y azulado ilustrado en la Imagen 2 tiene una masa justo en el borde de donde se puede apretar una bola de gas frío y aún esperar que se comporte como una bola de gas frío. La parte superior izquierda de la placa ilustra el maravilloso resultado si te mueves más allá de esto, a unos 75 Júpiter (24.000 masas terrestres): ¡se enciende la fusión de hidrógeno y el “planeta” comienza a brillar! Se ha convertido en una estrella enana.
Discutiremos qué es la fusión de hidrógeno y cómo genera grandes cantidades de energía nuclear, un poco más adelante. El punto importante aquí es que la generación de calor en las profundidades del planeta/estrella lo transforma radicalmente. Los superplanetas inertes simplemente se encogen a medida que acumula más masa, pero el calor en una estrella aumenta drásticamente la presión de sus gases y detiene cualquier contracción adicional. De hecho, la gran producción de energía de las estrellas más grandes, como nuestro Sol, hace que se hinchen en enormes (aunque ligeras y esponjosas) bolas mucho más imponentes que cualquier planeta. (Consulte la Imagen 3 para obtener más información sobre el Sol).
Sin embargo, el Sol y otras estrellas pueden mantener su volumen solo mientras tengan una fuente de calor para generar gas a alta presión, y ninguna fuente de calor puede durar para siempre. Dado que la compresión gravitacional es lo que nos interesa en este momento, dejemos de lado la generación de calor como un simple obstáculo temporal y sigamos adelante. Supongamos que tenemos un planeta/estrella de 75 MJ que no puede generar calor. ¿Qué sucede en ese caso, a medida que agregamos más masa?
Sigue encogiéndose, por supuesto. Para abreviar, los objetos masivos (sin fuente de calor) nunca dejan de encogerse a medida que se vuelven más masivos. Pero, a medida que avanzan hacia el reino de las 100 masas de Júpiter más o menos, cambian la forma en que se encogen.
A medida que los átomos de una estrella se presionan más juntos, eventualmente llegan a un punto donde las nubes de electrones de los núcleos adyacentes comienzan a superponerse. Esto hace que la física de la estrella dé un giro brusco hacia un territorio muy extraño, porque significa que la mecánica cuántica ahora está tomando las decisiones en lugar de la física clásica. El hecho de que los electrones sean realmente nubes y no objetos sólidos (ver Imagen 1) podría llevarlo a creer que sería fácil comprimir electrones juntos, y estaría muy equivocado. Los electrones son nubes de la mecánica cuántica, no bocanadas de aire, y resulta que la mecánica cuántica desaprueba severamente la superposición de nubes de electrones. (Esta desaprobación se conoce técnicamente como el Principio de Exclusión de Pauli, en honor al físico Wolfgang Pauli). No es fácil condensar una discusión sobre la teoría de la mecánica cuántica en unos pocos párrafos, pero afortunadamente, solo necesitamos cubrir algunos puntos clave.
Todo lo que necesitas saber sobre la mecánica cuántica de las estrellas
Los átomos están hechos de protones, neutrones y electrones. Los protones y neutrones forman los núcleos de los átomos y son muy densos, con un peso increíble de 1018 kg/m3. (Si toda la Tierra se comprimiera a densidades de protones/neutrones, solo tendría unos 700 pies de diámetro). Los núcleos atómicos se comportan así como partículas muy pequeñas pero muy pesadas. Los electrones son una olla de pescado diferente. Mucho menos densos que los protones o neutrones (por un factor de 1013), los escritores populares suelen decir que los electrones “orbitan” los núcleos atómicos, a pesar de que la mayoría de nosotros en la comunidad física abandonamos la noción de electrones de partículas puntuales en 1927. Como se explica en la Imagen 1, los electrones no son partículas como tales. Son entidades más complejas que actúan como ondas la mayor parte del tiempo, pero llevan masa e impulso discretos como si fueran partículas.
Ahora, la mecánica cuántica se llama mecánica cuántica porque las partículas elementales como el electrón normalmente están restringidas a ocupar estados de energía y momento (o niveles de energía, si se quiere) que existen solo en valores cuantificados específicos. Solo las partículas elementales que se mueven libremente en el espacio, interactuando con nada, pueden tomar cualquier energía de la misma manera que un automóvil en la carretera puede tomar cualquier velocidad. Para un electrón dentro de un átomo, los posibles estados de energía que puede ocupar son análogos a los de una caja en una escalera. (Vea la Figura 1 a la derecha). La caja puede estar en un escalón o en el siguiente, pero no puede descansar en ningún lugar intermedio. Al igual que la caja, un electrón puede rebotar “hacia abajo” espontáneamente por la escalera a un estado de menor energía, pero nunca puede “subir” las escaleras sin una entrada de energía del exterior. Sin embargo, a diferencia de la caja, el electrón siempre se moverá hacia abajo, tarde o temprano, con o sin ayuda externa. Y muy a diferencia de la caja, es imposible predecir cuándo el electrón podría hacer esto: todo lo que puede hacer es especificar una probabilidad de cuánto tiempo tardará. (Si desea llevar la analogía caja/escalera al extremo, entonces puede imaginar una caja con un conejo agitado encerrado dentro. Usted sabe que la caja tambaleante caerá por las escaleras eventualmente, pero no sabe cuándo).
Otra forma en que un electrón se diferencia de una caja es que dos cajas están felices de colocarse en el mismo paso, pero dos electrones no. En pocas palabras, dos electrones nunca pueden ocupar el mismo estado cuántico. Pueden y con frecuencia ocupan el mismo espacio, pero eso es diferente. (Imagínese dos nubes de humo de puros diferentes, mezclándose en el aire. A eso me refiero cuando digo que dos electrones pueden “ocupar” el mismo espacio. Ambos pueden tener alguna probabilidad de estar en el mismo punto). hacer es ocupar el mismo espacio y poseer simultáneamente la misma energía e impulso. En otras palabras, si las nubes de humo de cigarro realmente se comportaran como electrones, entonces se necesitarían nubes de humo de la misma temperatura y color para rebotar entre sí como rocas en lugar de mezclarse. Solo podían mezclarse si estaban a diferentes temperaturas o tenían diferentes colores. Si esto parece un poco extraño, bueno, dije que no era fácil explicar la mecánica cuántica en unos pocos párrafos. El punto principal aquí es que los electrones obedecen a una regla de exclusión que les prohíbe ocupar los mismos niveles cuánticos.
Sin embargo, normalmente esta regla de exclusión solo se aplica a los electrones que están dentro del mismo átomo. En el caso de la materia “normal” (como la de la que estás hecho), los electrones están unidos a núcleos que están esparcidos por el espacio dentro de ti como canicas esparcidas a millas de distancia. Hay mucho espacio para que la pequeña familia de electrones en cada átomo tenga los estados más favorables, es decir, la energía más baja, para sí mismos. (Consulte la Imagen 4 en la Ilustración).
Esta feliz disposición llega a su fin cuando las nubes de electrones comienzan a superponerse dentro de una estrella que colapsa. A medida que un porcentaje cada vez mayor de ellos se aplasta, las reglas de la mecánica cuántica exigen que solo uno de los billones de billones de billones de electrones que empujan en un centímetro cúbico permanezca en su estado original de menor energía. Piense en ello como una vivienda urbana: si la densidad de población es lo suficientemente baja, todas las familias pueden vivir en una casa estilo rancho. Pero cuando la densidad alcanza la de Manhattan, entonces alguien tiene que vivir a 62 pisos del suelo. Los electrones son más bien así, excepto peor. En la versión cuántica de Manhattan, ¡solo un electrón en toda la ciudad puede vivir en la planta baja! Los otros electrones deben ser empujados a estados de mayor energía, y dado que solo hay un electrón por estado, sin importar cuántos electrones haya, los electrones se elevan rápidamente a energías asombrosas. En promedio, los electrones de una estrella colapsada transportan 100.000 voltios de energía, lo que corresponde a una “temperatura de electrones” muy por encima de mil millones de grados Kelvin3 si piensa en los electrones simplemente como partículas en un gas caliente.4 (Es decir, 100.000 voltios es mucho más que suficiente para arrancar los electrones de los núcleos individuales, por lo que los electrones están libres de vagar de un lado de la estrella a otro como un gas). Los físicos dicen que la materia tiene condensado en un estado nuevo y peculiar llamado materia degenerada por electrones.
En este punto, nuestra estrella tiene quizás una cuarta parte de la masa solar (aproximadamente 80.000 masas terrestres), empaquetada en un volumen que no es mucho más del doble del radio de la Tierra. Ahora es tan denso que una botella de un cuarto de galón de materia degenerada por electrones cerca de su superficie pesaría 50 toneladas. Tales objetos no son en absoluto teóricos: la Vía Láctea contiene posiblemente diez mil millones de ellos, y el primero fue avistado en 1862. Los astrónomos se refieren a ellas como enanas blancas, porque son muy pequeñas y candentes. (¡El orgullo me obliga a señalar que el telescopio del Observatorio Dearborn de Northwestern fue el mismo instrumento utilizado para realizar el avistamiento histórico de 1862! La honestidad me obliga a admitir que Northwestern no adquirió el telescopio hasta 1887; en 1862 el telescopio todavía estaba en Boston, donde fue fabricado.)
Para la materia normal (gas, líquida o sólida), uno visualiza los átomos como sistemas solares en miniatura, con nubes de electrones “planetarios” que rodean a los “soles” nucleares. Se permite que algunos electrones se comporten como tranvías y se pueden compartir entre átomos vecinos para formar enlaces químicos, pero eso es todo. Para la materia degenerada por electrones, como se puede imaginar, esta imagen del “sistema solar” no funciona en absoluto. Los electrones en la materia degenerada están comprimidos tan juntos que se comportan más o menos como si toda la estrella fuera un gran sistema cuántico. Forman un gas de electrones y se comportan de manera muy similar a un fluido altamente presurizado dentro de la estrella. Los núcleos desnudos de electrones se comportan menos como “soles” y más como perdigones de plomo que atraviesan el gas de electrones.
Sorprendentemente, el movimiento de los núcleos casi no se ve afectado por este cambio en su entorno de electrones. Todavía se mueven como si estuvieran en un gas normal en lugar de uno degenerado por electrones. Hay dos razones para esto. Primero, los núcleos no son electrones. Las reglas que racionan la energía de los electrones son completamente irrelevantes para los protones5 y los neutrones6 que forman los núcleos. (Los protones y los neutrones tienen sus propios estados cuánticos, gracias.) En segundo lugar, los núcleos son mucho más densos y masivos que los electrones. A medida que los núcleos se mueven, son tan ajenos a los estados energéticos de los electrones como una bala de cañón a la humedad atmosférica.
Lo que esto significa es que, si calienta o enfría la materia degenerada por electrones, los núcleos se mueven más rápido o más lento tal como lo harían en un gas normal. Pero a diferencia de un gas normal, a los electrones no les importa y no siguen su ejemplo. Ya no están apegados a ningún núcleo en particular y, de hecho, el único factor que les afecta es la lucha por separarse más y evitar la regla de exclusión. Esa lucha resulta de la inmensa compresión creada por la inmensa gravedad de la enana blanca, y la gravedad no tiene nada que ver con la temperatura. Por lo tanto, el gas de electrones responde solo a los cambios en la masa de la enana blanca (es decir, a los cambios en su gravedad), y no a los cambios en su temperatura, lo que a su vez significa que una enana blanca no cambia de tamaño en absoluto como se calienta o enfría.
Este último hecho es muy crítico, como veremos más adelante. Los gases normales cambian de volumen cuando se calientan o enfrían, por lo que el aire caliente sube y el gas más frío desciende. Pero la materia degenerada por electrones se comporta más como un líquido exótico y fantásticamente denso que como un gas, y los líquidos no cambian mucho de volumen cuando se calientan. Solo se calientan más. Por tanto, la materia degenerada en electrones es mucho más difícil de comprimir que la materia normal. (Se necesita energía para elevar un electrón a un nivel superior, y elevar todos los electrones en algo con la masa de una estrella requiere mucha energía).
En resumen, cuando se trata de cómo reaccionan al aumento de presión o temperatura, las enanas blancas se comportan más como cuerpos “sólidos” como la Tierra que como cuerpos gaseosos como Júpiter o el Sol. Casi hemos cerrado el círculo en nuestra discusión sobre cuerpos masivos.

Casi.
En 1931, el astrofísico teórico Subrahmanyan Chandrasekhar (que entonces solo tenía 21 años) publicó un trío de artículos sorprendentes sobre la materia degenerada por electrones. Sus cálculos mostraron que a medida que una enana blanca se vuelve más masiva, inevitablemente debe acercarse a un punto crítico. Esto resulta ser una consecuencia de La teoría de la relatividad de Einstein, y dado que no puedo explicar la relatividad en un párrafo, solo resumiré los hechos: a medida que los electrones en una enana blanca se elevan a niveles de energía más altos, se mueven más rápido. Sin embargo, una de las leyes más fundamentales de la relatividad es que nada puede moverse más rápido que la velocidad de la luz (186,282 millas por segundo). A medida que las partículas se acercan a esta velocidad, es imposible acelerarlas porque comienzan a ganar masa a partir de la misma energía que las empuja. Esto está incorporado en la famosa ecuación, E = mc2, que establece que la energía se puede convertir en masa y viceversa. Aproximadamente hablando, las partículas cercanas a la velocidad de la luz ganan masa en lugar de energía, o para decirlo de otra manera, se vuelven más pesadas pero no van más rápido cuando se les agrega energía. (Uno no puede evitar pensar en un cerdo gordo, que ingiere mucha energía alimenticia pero se vuelve más gordo y más lento en lugar de más rápido y más poderoso). Usando este hecho, Chandrasekhar notó que la presión de electrones en una enana blanca debe tener un límite absoluto. Incluso si se aplastara a una densidad infinita, el límite de velocidad impuesto por la relatividad todavía forzaría un corte a cualquier presión que pudieran ejercer.
Al mismo tiempo, de manera alarmante, no hay límite para la cantidad de masa que se puede apilar sobre una enana blanca. Peor aún, cuanto más pesado lo haces, más poderosa se vuelve la fuerza gravitacional en su superficie. La famosa Ley de Gravitación Universal de Isaac Newton establece que la fuerza de gravedad es proporcional a 1/r2, lo que significa que si el radio de un planeta se reduce en un factor de dos, entonces la fuerza de gravedad en su superficie debe aumentar en un factor de cuatro.
Chandrasekhar mostró que había un punto en el que el avance ilimitado de masa creciente y radio decreciente ya no podía sostenerse. Como una pajita rompiendo el lomo de un camello, agregar más masa a una enana blanca en este punto haría que la compresión gravitacional de la enana exceda cualquier posible aumento en la presión de los electrones. Así, el enano se encogería, pero quedaría con un desequilibrio gravitacional aún peor que antes. El mayor desequilibrio haría que se encogiera aún más, agravando así la crisis gravitacional…
En resumen, los cálculos de Chandrasekhar predijeron que si una enana blanca se elevaba más allá de una masa crítica, ¡colapsaría catastróficamente! Calculó que esta masa crítica era aproximadamente 1,4 veces la masa del Sol, y con el tiempo llegó a conocerse como el Límite de Chandrasekhar.

Sería justo decir que esta noticia tuvo una recepción muy variada en 1931. La mecánica cuántica era todavía un tema muy joven en ese momento (solo cuatro años) y muchos astrofísicos todavía tenían serias dudas sobre toda la teoría de la mecánica cuántica, nunca tenga en cuenta la credibilidad de esta predicción en particular. ¿Cómo, se burlaron, podría un objeto la mitad de masivo que el Sol y ya comprimido a una densidad casi inimaginable, simplemente “colapsar”? Colapsar a qué? Fue completamente absurdo. Si se lleva a su conclusión lógica, el trabajo de Chandrasekhar indicaba que una enana blanca empujada por encima del límite desaparecería literalmente, o más exactamente, se comprimiría instantáneamente a un punto infinitesimal. No faltaron los astrónomos que se mostraron escépticos sobre esta idea, por decirlo suavemente. Sir Arthur Eddington, el primer astrónomo que verificó la predicción de Einstein de que la gravedad del Sol podría desviar la luz de las estrellas, y posiblemente el astrónomo más respetado de su tiempo, simplemente descartó la predicción. De hecho, fue en gran parte la crítica vocal de Eddington a la teoría lo que hizo que casi se ignorara durante la mayor parte de una década.
Y, sin embargo, para entonces, los astrónomos habían descubierto docenas de estrellas enanas blancas… y ninguno tenía una masa superior a 1,4 masas solares, hasta donde se pudo determinar. Hubo algunos que sintieron que esto estaba demasiado de acuerdo con el Límite de Chandrasekhar como para descartar toda la idea. Como veremos más adelante, la historia completa de lo que sucede cuando una enana blanca es llevada más allá de 1,4 masas solares resulta maravillosa y complicada, pero antes de que podamos contar esa historia debemos dirigir nuestra atención al nacimiento estelar, lo cual haremos en la siguiente sección.
Antes de continuar, señalaré que en 1937, cansado de la hostilidad hacia sus teorías de Eddington y otros astrónomos británicos, Chandrasekhar dejó Cambridge para ocupar un puesto en la facultad de la Universidad de Chicago, donde permaneció el resto de su vida. En 1983 fue galardonado con el Premio Nobel de Física, principalmente por su trabajo sobre las enanas blancas.
1 – Júpiter es el quinto planeta desde el Sol. Es el objeto más masivo del Sistema Solar a excepción del Sol mismo y, de hecho, dado que tanto Júpiter como el Sol están compuestos casi en su totalidad de hidrógeno y gas helio, Júpiter se parece mucho más al Sol que a la Tierra. Con diez veces el diámetro de la Tierra y con un peso de 318 masas terrestres, Júpiter es 2,4 veces más masivo que todos los demás planetas y lunas del Sistema Solar juntos. El autor Isaac Asimov bromeó una vez que “El Sistema Solar está formado por el Sol, Júpiter y un poco de escombros”.
2 – Para los puristas, este máximo teórico depende de varios supuestos, como si el planeta está compuesto mayoritariamente por hidrógeno y helio, o no. Para nuestros propósitos, una estimación de 1,7 masas de Júpiter es suficientemente buena.

Imagen 3
La notación 1018 solo significa que tienes un uno seguido de 18 ceros. De manera similar, 10–18 significa que tiene un cero, un punto decimal, luego 17 ceros y uno.
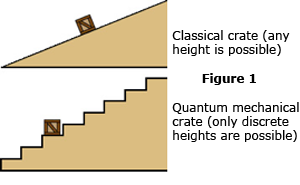
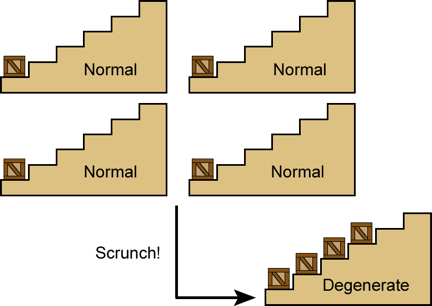
Imagen 4
3 – Los grados Kelvin son lo mismo que los grados Celsius, excepto que cero C° corresponde al punto de congelación del agua pura, mientras que cero K° corresponde al cero absoluto, la temperatura más fría posible. El cero absoluto es la temperatura teórica en la que cesa todo movimiento, incluso el movimiento atómico. Por lo tanto, la escala Kelvin a veces también se denomina escala de temperatura absoluta. El cero absoluto ocurre a 0 K°, o a -459,69 F°, como prefiera.
4 – El calor es simplemente el movimiento aleatorio de pequeñas partículas. Cuanto más enérgico es el movimiento de las partículas individuales, mayor es la temperatura del conjunto.
5 – El protón tiene carga positiva y es 1836 veces más masivo que un electrón. Los electrones tienen la misma carga que los protones, excepto que tienen un signo negativo, por lo que el número de electrones que rodean un núcleo debe ser igual al número de protones. Los electrones compartidos forman la química, por lo que el número de protones de un núcleo determina directamente su química. Cada elemento de la tabla periódica corresponde a un núcleo con un número de protones coincidente: el elemento # 8 (oxígeno) tiene ocho protones, y así sucesivamente.
6 – Los neutrones tienen casi exactamente la misma masa que los protones (los neutrones son un 0,06% más masivos) pero no tienen carga eléctrica, de ahí el nombre. La materia ordinaria consta de aproximadamente un 50% de protones y un 50% de neutrones, por lo que los neutrones encerrados dentro de los núcleos constituyen aproximadamente la mitad de la materia normal del Universo. Sin embargo, a diferencia de los protones, los neutrones libres no son estables. Fuera del núcleo, los neutrones se descomponen en un protón, un electrón y algo llamado antineutrino, en aproximadamente 10,6 minutos. Los neutrones libres no se detectaron hasta 1932.

Recent Comments