Königsbergin sillat
Original web-page: http://www.efgh.com/math/koenigsberg.htm
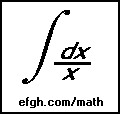
Philip J. Erdelsky
9 de junio de 2015
Uno de los problemas clásicos de la matemática son los puentes de Königsberg, que fue resuelto por el matemático suizo Leonhard Euler en el siglo XVIII. Es fácil de declarar y bastante fácil de resolver.
Un río pasa por la ciudad de Königsberg (ahora Kalingrad). En el río hay dos islas. Siete puentes conectaban las islas y los bancos, como se muestra en este mapa antiguo:
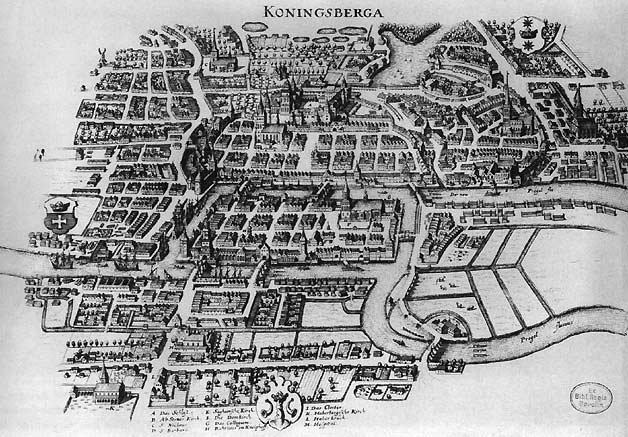
Los dos canales del río se unen en algún lugar del lado derecho del mapa.
Mucha gente intentó caminar alrededor de Königsberg, cruzando cada puente una y solo una vez, pero nadie pudo hacerlo. Euler demostró que la tarea es imposible. Su demostración requiere solo algunos conocimientos básicos de aritmética y las propiedades de los números pares e impares.
La brillante visión de Euler, si se puede llamar así, fue contar la cantidad de las TERMINAS de puentes conectados a cada terreno:
- 3 en la orilla norte
- 3 en la orilla sur
- 5 en la isla en el centro del mapa
- 3 en la isla en el lado derecho del mapa
Un paseo que cruza cada puente una vez y solo una vez se llama, adecuadamente, un paseo de Euler (o un camino de Euler).
Si una caminata de Euler no comienza o termina en un terreno en particular, entonces debe haber un NÚMERO PAR de puentes conectados a ella, porque un caminante de Euler que ingresa al área por un puente debe dejarla por otro. Si una caminata de Euler comienza o termina en un terreno en particular, entonces el número de puentes conectados debe ser IMPAR.
Dado que cada uno de los cuatro terrenos tiene un número impar de puentes conectados, es obvio que una caminata de Euler es imposible.
Los puentes de Königsberg es un ejemplo de una estructura matemática general llamada gráfica.
Un gráfico consta de un número finito de vértices (también llamados nodos), correspondientes a los terrenos en los Puentes de Königsberg, y un número finito de aristas (también llamadas líneas), correspondientes a los puentes. Continuaremos llamándolos puentes. Además, para evitar dificultades con caminatas inexistentes, requerimos que haya al menos un vértice.
Aquí hay una representación más abstracta del gráfico de Königsberg:
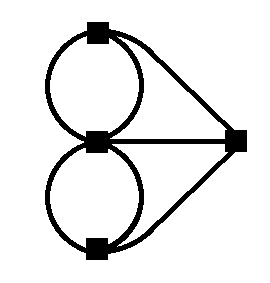
Un gráfico puede ser más general que los puentes de Königsberg. Por ejemplo, un puente puede conectar un vértice consigo mismo y no es necesario que los vértices estén confinados a un solo plano. También es posible un vértice aislado, sin puentes de conexión.
El número de puentes que conectan un vértice en particular se denomina grado (o valencia).
Los argumentos de Euler mostraron que una caminata de Euler es posible solo si (1) todos los vértices son de grado par, en cuyo caso la caminata comienza y termina en el mismo vértice, o (2) dos vértices, donde comienza y termina la caminata, son de grado impar y todos los demás vértices son de grado par.
Son obvias dos propiedades de los paseos de Euler. El reverso de una caminata de Euler es una caminata de Euler, y si una caminata de Euler comienza y termina en el mismo vértice, también puede comenzar y terminar en cualquier otro vértice.
¿Son estas condiciones también suficientes? Obviamente no. El gráfico también debe estar conectado, es decir, debe haber algún camino (no necesariamente un camino de Euler) de cada vértice a cada otro vértice.
Demostrar la existencia de una caminata de Euler para un grafo conectado sin vértices de grado impar o dos vértices de grado impar es algo más difícil, pero no involucra matemáticas avanzadas.
Primero, considere un gráfico conectado donde todos los vértices son de grado par. Empiece a caminar en un vértice, haciendo un seguimiento de los puentes que ha cruzado. Cada vez que ingrese a un vértice, déjelo junto a un puente que no haya cruzado anteriormente. Si no es el vértice inicial, entonces si ingresó por un puente sin cruzar, siempre puede dejarlo por otro. Y después de que te vayas, el vértice todavía tiene un número par de puentes sin cruzar.
La caminata debe llegar a su fin cuando regrese al vértice inicial y no pueda encontrar un puente sin cruzar para dejarlo.
Si ha logrado cruzar todos los puentes, la caminata está terminada.
Si todavía hay al menos un puente sin cruzar, se debe aumentar la caminata.
Sin embargo, observe que cada vértice todavía tiene un número par de puentes sin cruzar.
Dado que la gráfica está conectada, hay un camino desde el vértice inicial hasta un vértice con un puente sin cruzar. Considere el primer vértice de este camino con un puente sin cruzar. Debe estar en la caminata. Llámalo vértice A.
Ahora comienza en el vértice A y haz una segunda caminata, cruzando solo los puentes que aún no has cruzado, ya sea en esta caminata o en la primera. Como anteriormente, la caminata termina solo cuando regresa al vértice A.
Ahora combine los dos paseos en uno solo. La forma más fácil de hacer esto es comenzar la primera caminata en el vértice A. Cuando regrese al vértice A, realice la segunda caminata.
Si todavía hay al menos un puente sin cruzar, puede continuar este proceso hasta que se hayan cruzado todos los puentes.
Podría preguntar qué sucede si la gráfica tiene solo un vértice y al menos un puente. Es fácil mostrar que la gráfica está conectada, que el vértice tiene un grado par y que hay una caminata de Euler. Un gráfico con un solo vértice y sin puentes no es necesariamente una excepción, aunque los conceptos de conectividad y paseos de Euler son algo vacíos en este caso.
Este es el resultado deseado para un gráfico conectado en el que cada vértice es de grado par. Ahora considere una gráfica con dos vértices B y C de grado impar. Cree un gráfico un poco más grande insertando un puente que conecte los vértices B y C. Todos los vértices en este gráfico son de grado par, por lo que tiene una caminata de Euler. Una parte de esta caminata implica cruzar el nuevo puente desde el vértice B al vértice C, o viceversa.
Está claro que este paseo de Euler, sin el nuevo cruce entre los vértices B y C, es un paseo de Euler en el gráfico original.
Recent Comments