Experimentos en perspectiva inversa

Experimentos en perspectiva inversa

Original web-page: http://paulbourke.net/miscellaneous/reverseperspective/

Escrito por Paul Bourke
Julio de 2020

Diapositivas de presentaciones

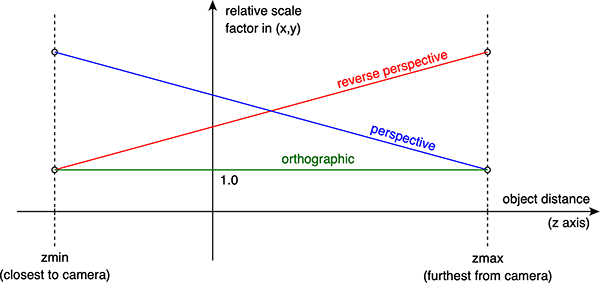
A modo de introducción, consideremos el modelo de una cámara virtual en gráficos por computadora y un objeto 3D, digamos un cubo. Los dos parámetros clave que determinan el tamaño del objeto en el plano de proyección de la cámara son la posición de la cámara con respecto al objeto y el campo de visión de la cámara. Ambos se pueden ajustar para controlar qué tan grande aparece el objeto en el plano del proyecto, siendo una región limitada de este plano la imagen resultante. Cuanto más cerca está la cámara del objeto, más grande debe ser el campo de visión para que el objeto llene el plano de la imagen. Si la cámara está muy lejos del objeto, entonces se requiere un campo de visión más pequeño para llenar el plano de la imagen con el objeto.

Imagínese entonces, comenzando con la cámara cerca del objeto con un gran campo de visión. En esta posición, los efectos de la perspectiva, el grado en que las partes distantes del objeto parecen más pequeñas que las partes más cercanas, será el más pronunciado. A medida que la cámara se aleja y el campo de visión se reduce para mantener el objeto del mismo tamaño en el encuadre, los efectos de la perspectiva se reducen. En el límite con la cámara al infinito, el campo de visión se puede imaginar como cero, no hay efectos de perspectiva y decimos que la proyección es ortográfica o paralela.

¿Se puede continuar este proceso de alguna manera para que los efectos de perspectiva se inviertan, es decir, las partes del objeto más cercanas a la cámara parezcan más pequeñas que las partes del objeto más alejadas de la cámara? La respuesta es sí, se llama perspectiva inversa o invertida y es el tema de esta discusión.

En lo que sigue se presentarán varios ejemplos. En cada caso, los objetos se renderizan tres veces, como perspectiva estándar (P > 0), ortográfica (P = 0) y finalmente perspectiva inversa (P < 0). Los tres primeros muestran el cubo de arriba con una perspectiva de 1, 2 y 3 puntos.

Punto único

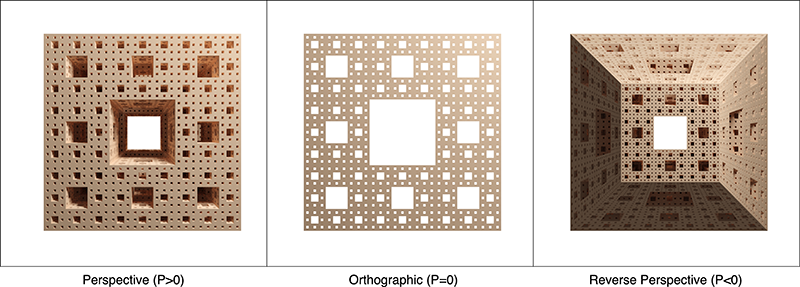
Dos puntos

 

Tres puntos

Otra forma de pensar en esto es considerar el grado en que las partes de un objeto se escalan en función de su distancia a la cámara. A continuación, imagine la cámara en el eje z negativo mirando hacia el origen. La escala relativa entre la parte más cercana del objeto y la parte más lejana del objeto se muestra para las tres proyecciones consideradas aquí. Tenga en cuenta que en lugar de las partes más cercanas y más lejanas de los objetos, también se puede usar el plano de corte cercano y lejano de la vista frustum. Tenga en cuenta que esta es una pista para una implementación de OpenGL/DirectX utilizando un sombreador de vértices.

 

Para aquellos familiarizados con la construcción de la perspectiva en el dibujo o la arquitectura tradicionales, la perspectiva inversa se construye colocando el objeto/escena entre el punto proyectivo y el plano de visualización/dibujo. En comparación con la construcción de perspectiva lineal tradicional donde el punto proyectivo está en el lado opuesto del plano de visión al objeto o escena.

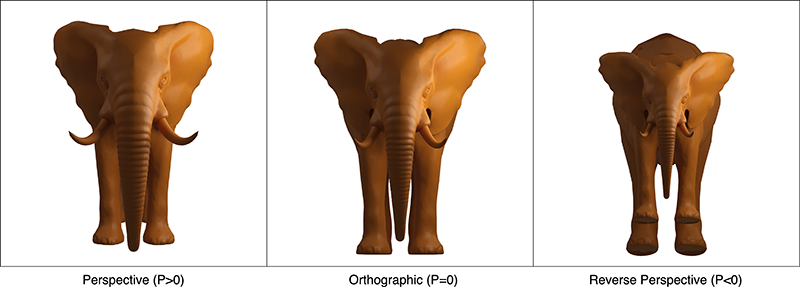
A continuación se da una idea de lo que les sucede a las cabezas, a medida que aumenta el factor de perspectiva inversa, se ven más y más partes de la cabeza normalmente oscurecidas. Esto es característico de muchas de las cabezas desde la perspectiva inversa en las pinturas bizantinas.

Hay muchos ejemplos de perspectiva inversa en el arte histórico. Sin embargo, no están necesariamente construidos en el sentido que se utiliza aquí, es decir, que las líneas de proyección divergen con la distancia, de modo que los objetos más distantes parecen más grandes. Por ejemplo, en algunos casos los objetos distantes más grandes se deben a una proyección anamórfica, de modo que el tamaño parece correcto si uno está parado en la posición “correcta”, la llamada perspectiva inversa solo ocurre para otras posiciones de visualización. Otro conjunto de perspectivas aparentemente inversas se puede atribuir a que las figuras distantes son más grandes debido a su mayor importancia.

Un par de ejemplos de perspectiva inversa citados a menudo se ilustran arriba, pero existe cierto debate sobre si esa era la intención o si lo que parece una perspectiva inversa simplemente surgió debido a la falta de consideración de la perspectiva actual combinada con los objetivos de composición. Si bien se dibujan algunos ejemplos de líneas que se desvanecen en el mismo lado del espectador, hay otros aspectos que no son consistentes con la perspectiva inversa.

Con respecto a la iconografía religiosa rusa y bizantina, escribe Pavel Florensky.

“Siempre resulta que los iconos que son más creativos en términos de percepción artística inmediata son ‘defectuosos’ en perspectiva, mientras que los iconos que satisfacen mejor el libro de texto de perspectiva son aburridos y desalmados. Si te permites simplemente olvidar las demandas formales de la interpretación en perspectiva por un tiempo, el sentimiento artístico directo llevará a todos a admitir la superioridad de los iconos que transgreden las leyes de la perspectiva”.

Referencias

• Clemena Antonova, “On the Problem of “Reverse Perspective”: Definitions East and West”. Leonardo, Vol. 43, No. 5 (2010), pp. 464-469
• Rudolf Arnheim, “Inverted Perspective in art: display and expression,” Leonardo 5 (1972) p. 125.
• Boris Raushenbach, “Perceptual Perspective and Cezanne’s Landscapes,” Leonardo 15 (1982) p. 32.
• Boris Raushenbach, “On My Concept of Perceptual Perspective that accounts for Parallel and Inverted Perspective in Pictorial Art,” Leonardo 16 (1983) p. 28.
• Jan Deregowski, Denis Parker and Manfredo Massironi, “The Perception of Spatial Structure with oblique Viewing: an explanation of Byzantine Perspective?” Perception 23 (1994) p. 5.
• Howard, Ian P.; Allison, Robert S. (2011), “Drawing with divergent perspective, ancient and modern”, Perception, 40: 1017–1033, doi:10.1068/p6876.

Visualización adicional

• Perspectiva inversa, Pavel Florensky, Beyond Vision.
• Pinturas en perspectiva inversa de Patrick Hughes.
• Óptica hipercéntrica: una lente de cámara que puede ver detrás de los objetos.
• Tamas Waliczky: video instalación “La manera”, 1995
• JMS, verdadera perspectiva inversa.
• Obras de David Belmonte.
• perspectiva inversa, Video de David Rafael Belmonte Caro
• EL ICONO: VERDAD Y FABLAS – Capítulo 4 – Perspectiva “inversa”