Estadísticas: ¿Cuántos revisarías?

Estadísticas: ¿Cuántos revisarías?

Original web-page: https://blog.jpalardy.com/posts/statistics-how-many-would-you-check/

JONATHAN PALARDY

9 de abril de 2015

Imagina esta situación:

Acaba de realizar una actualización por lotes en millones de usuarios en su base de datos. No hubo mensajes de error y está seguro de que todo salió bien. Pero no estaría mal comprobar…

¿Cuántos usuarios tendría que verificar para sentirse seguro de que todo funcionó para al menos el 95% de los usuarios?

Aquí están algunas ideas:

• si usted no marca, no se sabe: la confianza es 0%. Después de todo, tal vez su actualización por lotes no funcionaba en absoluto, pero no había ningún mensaje de error.
• si revisas todo, usted sabe la respuesta: la confianza es del 100%. Pero eso podría ser un montón de trabajo…
• si revisas algunos usuarios, tal vez 10, y la actualización trabajado… se puede empezar a sentirse bien. ¿Qué confianza puede ser?

No creo que la respuesta es obvia. Tenía que tomar algún tiempo para pensar en ello.

Un desvío: valoración media

Recordé haber leído Cómo no ordenar por calificación media, y pensé que podría aplicar la misma lógica a este problema.

Si solo tienes una revisión, y es positiva, ¿es eso 100%? Intuitivamente, sabemos que no lo es: es solo la opinión de una persona. A medida que más y más personas dan evaluaciones positivas, podemos comenzar a sentirnos mejor acerca de la precisión de la puntuación.

La cita del artículo es:

Dadas las calificaciones que tengo, hay un 95% de probabilidad de que la fracción “real” de las calificaciones positivas sea al menos qué?

Podemos usar el límite inferior del intervalo de confianza de Wilson.

En la práctica, con R

binom.wilson función, del paquete binom se puede utilizar de esta manera:

> binom.wilson(18, 20)
    method  x  n mean     lower     upper
  1 wilson 18 20  0.9 0.6989664 0.9721335

En otras palabras, si muestreamos 18 positivos y 2 negativos (18/20), la fracción “real” probablemente se encuentre entre 0.699 y 0.972 (media: 0.9).

Para nuestro ejemplo, podríamos invocarlo con 100% de éxito:

> binom.wilson(10, 10)
    method  x  n mean     lower upper
  1 wilson 10 10    1 0.7224672     1

El límite superior no es interesante: no estamos interesados en el mejor escenario posible. Pero si marca 10 y todos tienen éxito, puede estar seguro de que funcionó para el 72.2% de los usuarios (límite inferior).

Si seguimos comprobando y seguimos encontrando éxitos, podemos sentirnos cada vez más seguros sobre el éxito “verdadero”:

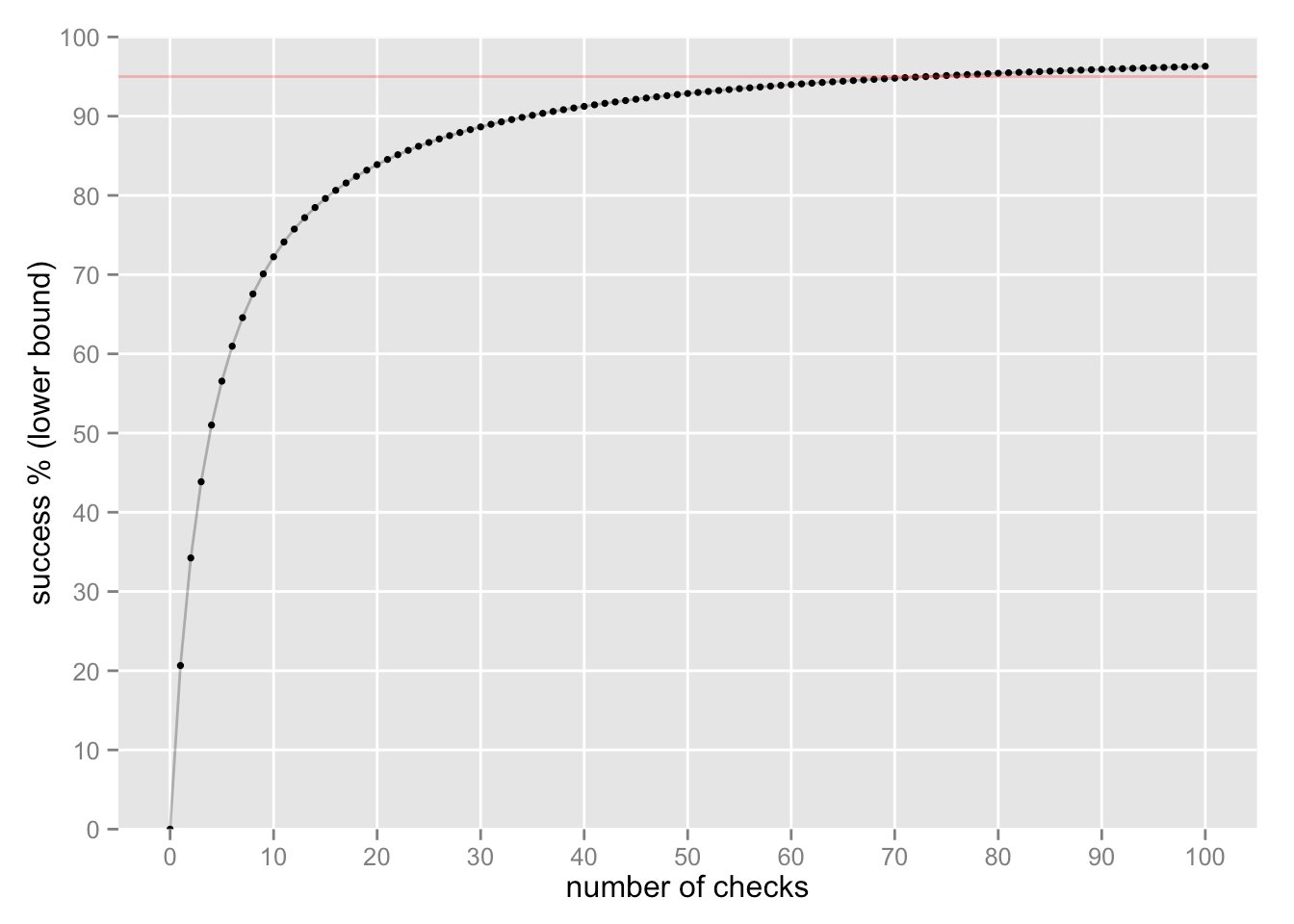
Se requieren 73 controles para alcanzar un límite inferior del 95% del éxito “verdadero” (la línea roja).

Análisis

Aquí está el análisis como un documento RMarkdown y la salida resultante documento html.

About the Author

admin